‘’Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lighting travel in a straight line’’
-Benoit Mandelbrot
Fraktallar, daha matematikte çok yeni bir konu olmasına rağmen aslında dünyanın oluşumundan bile önce evrende varlığını sürdürüyordu. Matematiğin yanında sanatla da oldukça iç içe olan bu konunun tanımı şöyledir : Fraktallar, matematikte, çoğunlukla kendine benzeme veya oransal kırılma özelliği gösteren karmaşık geometrik şekillerin ortak adıdır. Ve klasik geometrideki üçgen, daire, kare gibi şekillerden oldukça farklıdır. Bir şeklin fractal olması için iki önemli şeye ihtiyacı vardır : self- similarity(kendi içinde benzerlik) ve non-integer dimension(tam sayı olmayan boyut).
Fraktallardaki her adım kendi içinde bir önceki ve sonraki adımla birebir aynıdır ve bu duruma self-similarity denir. Fakat, non-integer dimension anlaması biraz daha zor olacağı için (açıklaması da bir o kadar zor) tanımını yaparken linkini aşağıda bulabileceğiniz makaleden direkt çeviri yapacağım. Klasik geometri, tam sayı olan boyutlarla ilgilenir mesela nokta sıfır boyutlu, doğrular bir boyutlu, kare ve üçgenler iki boyutlu, küreler ve küpler üç boyutludur. Ancak, bir çok doğal fenomen iki tam sayı arasındaki boyutlar kullanılarak daha iyi tanımlanır. Düz bir doğru bir boyuta sahipken, fractal curve(eğrisi) bükülme ve eğrilme durumuna göre ne kadar yer kapladığına bağlı olarak bir ile iki arasında bir boyuta sahip olacaktır. Düz bir fractal düzlemi ne kadar doldurursa, iki boyutlu olmaya o kadar yaklaşır. Makaledeki tanımın pek açıklayıcı olmadığının farkındayım ama sözlü olarak bulabildiğim en iyi tanımdı. Şimdi non-integer dimension’ın matematiksel ispatını basitçe yapmaya çalışacağım ve eminim bu ispat daha anlaşılır olacaktır:
Öncelikle, doğruların bir boyutlu ve kare, üçgen gibi şekillerin iki boyutlu olduğunu biliyorduk. İddiamıza göre Koch curve (veya fractal eğrisi) bir ile iki boyut arasında bir yerde bulunuyor.
–Koch curve
Şimdi, eğer bir doğruyu(bir boyutlu) sürekli ikiye bölersek(bisect) her seferinde 2 kat fazlası kadar ve bir önceki adıma oranı ½ olan yeni doğrular elde ederiz. Peki bir kareyi(iki boyutlu) sürekli ikiye bölersek her seferinde 4 kat fazlası kadar ve bir önceki adıma oranı ¼ olan yeni kareler elde ederiz. Eğer üç boyutlu şekiller için ikiye bölme yaparsak 8 kat fazlası kadar ve bir önceki adıma oranı 1/8 olan yeni üç boyutlular elde ederiz. Bu sıra böyle uzayıp gidiyor. Peki ya bu bir, iki, üç veya dört boyutlu şekilleri üçe bölersek(trisect) ne olur? Cevap oldukça belli. Bir boyutlular 3 kat fazlası kadar 1/3 oranında, iki boyutlular 9 kat fazlası kadar 1/9 oranında ve 3 boyutlular 27 kat fazlası kadar 1/27 oranında yeni şekiller oluştururlar. Şimdi aşağıdaki tabloyu inceleyelim. (Aşağıdaki işlemlerde (*) işareti üssü anlamında kullanılmıştır.)
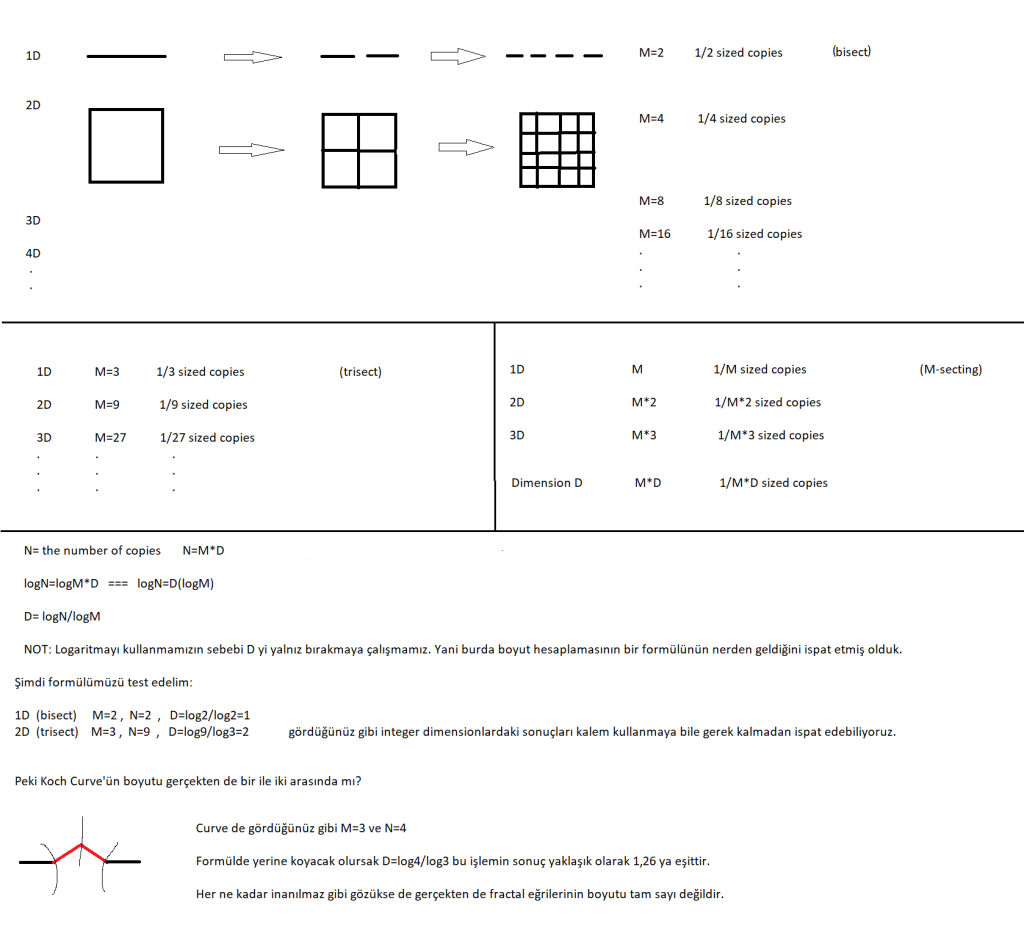
Umarım matematiksel ispatı konuyu anlamanıza tanımını yapmaktan daha çok yardımcı olmuştur. Bu işlemlerin sonucunda curve ne kadar ileri götürülse N ve M değerlerindeki orantısız artış yüzünden şekil iki boyutlu olmaya çalışacaktır. Eğer olayı tersinden düşünecek olursak; bir doğruyu sürekli iki veya üç eşit parçaya bölmeye devam edersek ve limitini alırsak(yani bu işlemi sonsuz kere tekrar edebildiğimizi düşünürsek) o doğruyu oluşturan her bir noktayı elde ederiz. Bu aslında bize non-integer dimension’ın varlığını ispatlamıyor fakat boyutlar arası geçişlerin olduğunu ve haliyle arada herhangi bir boşluğun olmadığını düşünmemizi sağlıyor.
Matematiğin her alanında olduğu gibi fraktallar da bilimde ve günlük hayatta bir çok yerde kullanılıyor. Bunlardan birkaçı astrofizik, biyoloji ve bilgisayar grafikleri.
Astrofizikte yıldızların uzayda dizilimini anlamaya çalışmakta veya gökyüzündeki bulutların şekillerinin modellemesinde kullanılıyorken biyolojide ise kromozomların ve DNA ların yapısında kendisini gösteriyor. Bilgisayar grafiklerinde ise filmlerde kullanılan efektler veya reklamlarda kullanılan doğa temasında daha gerçekçi bir görünüm yakalamak için önemli ölçüde rol alan fraktallar bilgisayarların icadından önce İngiliz kartograflar tarafından sahillerinin haritalanmasında kullanılmıştı.
Hayatımızın her alanında olan fraktallar, insanların gözünde basit bir rastlantıdan ibaret gibi gelebilir fakat bu rastlantı olması gerektiğinden daha gerçek ve hiçbir matematiksel denklem belki de asla bu rastlantıların tanımını mükemmel olarak yapamayacaktır.
http://www.fractal.org/Bewustzijns-Besturings-Model/Fractals-Useful-Beauty.htm
https://www.tandfonline.com/doi/pdf/10.1080/0020739920230108

Yorum bırakın