Yeryüzüne ya da gökyüzüne dikkatlice baktığınızda hemen hemen her şeyde bulunan bir benzerlik ya da şekiller arasında göze hoş çarpan bir oran olduğunu fark etmişsinizdir. Fibonacci sayıları işte burada devreye giriyor. 1,1,2,3,5,8,13,21,34,55… bir sonraki terim kendinden önceki iki terimin toplamı şeklinde giden bu sayı dizisi; ayçiçekleri, ananaslar, papatyalar ve hatta sadece bitkilerde değil evrende bulunan hemen hemen çoğu şeyde varlığını bize gösteriyor. Bu gizemli sayılardaki mucizeler sadece bu kadarla da sınırlı değil. Eğer bu sayı dizisinin karesini alacak olursak: 1,1,4,9,25,64,169,441,1156,3025… 2. dizideki ilk iki terimin toplamı 1. dizideki üçüncü terime eşit veya 2. dizideki üçüncü ve dördüncü terimlerin toplamı 1. dizideki yedinci terime eşit çıkıyor ve bu durum böyle devam ediyor. Başka bir örnek verecek olursak 2. Dizideki yani Fibonacci sayılarının karesi olan dizideki terimleri sırayla art arda toplarsak:
1+1+4=6
1+1+4+9=15
1+1+4+9+25=40
1+1+4+9+25+64=104
Bu sayılar içinde Fibonacci gizli.
6=2×3
15=3×5
40=5×8
104=8×13
Peki bulunan bu sayılar rastgele mi bulunuyor yoksa bunların temelinde bir mantık gizli mi?
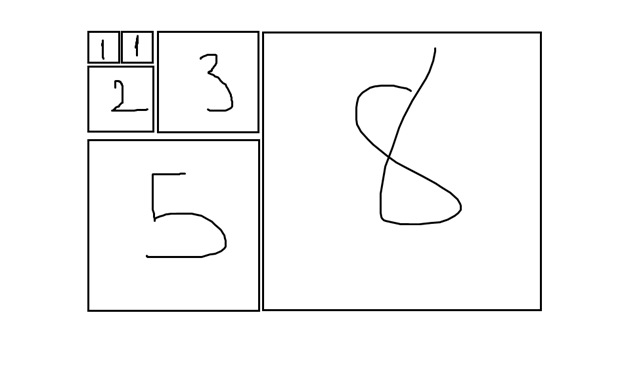
Yukarıda görülen bu parçalara ayrılmış karelerin içinde yazan sayılar bir kenar uzunluğunu gösteriyor. Şimdi burada basit bir alan hesabı yapalım: (1*2)+(1*2)+(3*2)+(5*2)+(8*2)= 8x(8+5). Bu eşitlikten de anlayacağınız üzere Fibonacci sayılarında karelerini alıp topladığımızda ortaya çıkan oran aslında geometriyle de doğrudan alakalı. Bu sayıları birbirine bölersek ortaya çıkan sonuç bize Fibonacci sayı dizisinin gittikçe altın orana yaklaştığını söyleyecektir. Şöyle ki:
13/8=1.625
21/13=1.61538
34/21=1.6190
55/34=1.6176
89/55=1.6181… Altın Oran=1.618033…
Bildiğiniz gibi altın oran aklınıza gelebilecek her yerde kullanılıyor. Fakat durumu tuhaf kılan şey zamanında teknoloji daha bu kadar ilerlememişken insanlar nasıl altın orana inanılmaz yakın olacak şekilde sonuçlar elde edebiliyorlardı? Matematiğin sadece hesaplama ve uygulama üzerinde olmadığını, bir diğer ve en önemli özelliğinin ilham almak olduğunu bize gösteren Fibonacciye sonsuz teşekkürlerimi sunarım.

Yorum bırakın