Eğer sonsuza kadar giden doğal sayıları ardı ardına toplarsanız (1+2+3+4…) sonuç -1/12 çıkacaktır. Matematikte Ramaujan Toplamı olarak bilinen bu anomali sayılabilir sonsuzlukta yapılan bir işlem olup Hindistanlı matematikçi olan Srinivasa Ramanujan tarafından ispatlanmıştır. Sonsuzluğu bilen adam olarak adını matematik tarihine kazıyan Ramanujan’ın bulduğu bu dizi sayesinde günümüzde teorik fizik ve ileri matematikte oldukça yaygın olarak kullanılıyor olup bunun yanında sicim teorisi ve kuantum teorisi için de işe yarar sonuçlar elde etmiştir. Şimdi bu Ramanujan toplamının ispatına gelecek olursak en başta bilmemiz gereken şey dizilerdeki yakınsak ve ıraksak olma durumudur. Kısaca bir dizi yakınsak ise herhangi bir limiti vardır ve o dizide dört işlem yapabiliriz fakat eğer ıraksak bir diziden bahsediyorsak bunları yapamayız. Mesela 1 den başlayarak bütün sayıları toplamaya çalışırsak işlemin içine sonsuzluk gireceği için arap saçına dönen bir işlem olacaktır. Ama Cesàro toplamı sayesinde bu karışıklığın içinden de çıkıyoruz ve sonuç olarak şu formülü buluyoruz:
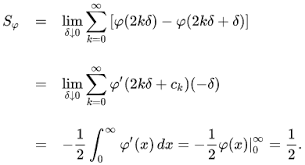
Ramanujan toplamında ise orijinal serimiz olan 1+2+3+4+… ün sonsuza gittiğini biliyoruz ve bunun için Cesàro toplamının da işe yaramayacağını biliyoruz çünkü limiti olan bir diziden bahsediyoruz.
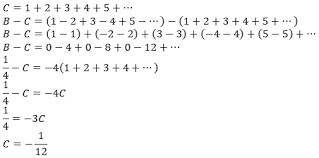
Bu işlemde C bizim orijinal serimiz olurken B ise yardımcı seri olarak faaliyet gösteriyor ve bu kadar basit bir işlemle orijinal serinin yani doğal sayıların toplamının -1/12 olduğunu kolayca ispatlayabiliyoruz.
Yorum bırakın